1716. Can
you answer these queries - 3
You are given an integer
sequence a1, a2, ..., an (|ai|
≤ 10000, 1 ≤ n ≤
50000). On this sequence you have to apply m
(m ≤ 50000) operations:
·
modify the i-th
element of the sequence
·
for given x and y print MAX {ai + ai+1
+ ... + aj, x ≤ i ≤ j ≤ y}
Input. The first line contains the integer n. The following line contains n
integers, representing the sequence a1,
a2, ..., an. The third line contains
the integer m. The next m lines contain the operations in
following form:
·
0 x y: modify ax into y (|y| ≤ 10000).
·
1 x y: print MAX {ai + ai+1 + ... + aj, x ≤ i ≤ j ≤ y}
Output. For each query, print an integer as the problem required.
|
Sample
input |
Sample
output |
|
4 1 2 3 4 4 1 1 3 0 3 -3 1 2 4 1 3 3 |
6 4 -3 |
РЕШЕНИЕ
структуры данных – дерево отрезков
Анализ алгоритма
Для решения задачи следует
реализовать нетривиальное обобщение дерева отрезков. В каждой его вершине будем
хранить четыре величины: сумму summa на
этом отрезке, максимальную сумму prefix
среди всех префиксов этого отрезка, максимальную сумму suffix среди всех суффиксов, а также максимальную сумму max подотрезка на нём. То есть для
каждого отрезка ответ будет предпосчитан не только для него, но и для отрезков,
упирающихся в его левую и правую границы.
В задаче также следует
реализовать модификацию одного элемента последовательности, одновременно с
изменением которого будут пересчитываться все четыре дополнительные величины во
всех узлах дерева отрезков, ведущих от соответствующего листа к корню.
Пример
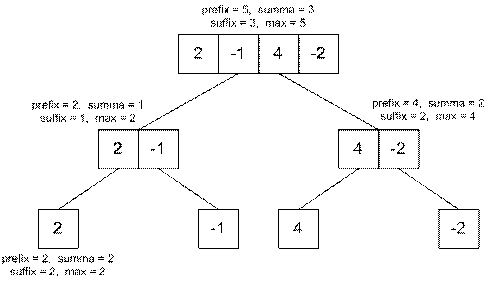
Рассмотрим массив {2, -1,
4, -2} и построим из него дерево отрезков. В каждой вершине вычисляем значения
дополнительных величин. В листах дерева их значения равны самому элементу
массива.
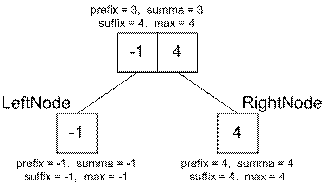
Вычислим суммы элементов на отрезке [1..2]. Для этого следует совершить
вызов функции GetMax(1, 0, 3, 1, 2). Разобъем отрезок [1..2] на два
фундаментальных: [1..1] и [2..2]. Рекурсивно найдем значения величин на каждом
их них (они являются листами, поэтому все значения равны между собой и равны
элементу массива), после чего совершим сборку двух отрезков.
Реализация алгоритма
#include <cstdio>
#include <algorithm>
#define MAX 50100
using namespace std;
struct node
{
int summa, prefix, suffix, max;
} SegTree[4*MAX];
int mas[MAX];
node Merge(node &Left, node
&Right)
{
node Res;
Res.prefix = max(Left.prefix,Left.summa + Right.prefix);
Res.suffix = max(Right.suffix,Right.summa + Left.suffix);
Res.summa = Left.summa + Right.summa;
Res.max = max(max(Left.max,Right.max),Left.suffix + Right.prefix);
return Res;
}
void build(int *a, int Vertex, int
LeftPos, int RightPos)
{
if (LeftPos == RightPos)
{
SegTree[Vertex].max = SegTree[Vertex].prefix =
SegTree[Vertex].suffix
= SegTree[Vertex].summa = a[LeftPos];
}
else
{
int Middle = (LeftPos + RightPos) / 2;
build (a, 2*Vertex, LeftPos, Middle);
build (a, 2*Vertex+1, Middle+1, RightPos);
SegTree[Vertex] = Merge(SegTree[2*Vertex], SegTree[2*Vertex+1]);
}
}
struct node GetMax(int Vertex, int LeftPos, int
RightPos,
int Left, int
Right)
{
if ((Left == LeftPos) && (Right == RightPos))
return SegTree[Vertex];
int Middle = (LeftPos + RightPos) / 2;
if (Right <= Middle )
return GetMax(2*Vertex,LeftPos,
Middle,Left,Right);
if (Left > Middle)
return
GetMax(2*Vertex+1,Middle+1,RightPos,Left,Right);
struct node LeftNode
=
GetMax(2*Vertex,LeftPos,Middle,Left,Middle);
struct node RightNode =
GetMax(2*Vertex+1,Middle+1,RightPos,Middle+1,Right);
return Merge(LeftNode, RightNode);
}
void Update(int Vertex, int LeftPos, int
RightPos, int pos, int
Value)
{
if (LeftPos == RightPos)
{
SegTree[Vertex].max = SegTree[Vertex].prefix =
SegTree[Vertex].suffix = SegTree[Vertex].summa = Value;
return;
}
int Middle = (LeftPos + RightPos) / 2;
if (pos <= Middle) Update(2*Vertex, LeftPos,
Middle, pos, Value);
else
Update(2*Vertex+1, Middle+1, RightPos, pos, Value);
SegTree[Vertex] = Merge(SegTree[2*Vertex], SegTree[2*Vertex+1]);
}
int i, L, R, n, m, type, pos, Value;
struct node res;
int main(void)
{
scanf("%d",&n);
for(i = 0; i < n; i++)
scanf("%d",&mas[i]);
build(mas,1,0,n-1);
scanf("%d",&m);
for(i = 0; i < m; i++)
{
scanf("%d",&type);
if (type)
{
scanf("%d %d",&L,&R);
res = GetMax(1,0,n-1,L-1,R-1);
printf("%d\n",res.max);
}
else
{
scanf("%d %d",&pos,&Value);
Update(1,0,n-1,pos-1,Value);
}
}
return 0;
}